
20210309_TIL
- 어제 정리한 자료구조, 알고리즘, 프로그래밍 언어라는 큰 틀에서 알고리즘 문제를 바라보는 시도를 했다. 하단 오늘 푼 문제 설명에 이 관점을 적용해 보았다.
- 재귀 함수, 정렬, 이분탐색 관련한 백준 문제들을 풀며 관련 개념을 익혔다. 아주 어려운 개념이 아닌 이상 문제에서 요구하는 코드의 80% 정도는 구현이 가능한 수준이 되었다. 이게 가능한 이유는 두 가지가 있을 것 같다. 1) 입력과 출력 관련한 코드 구현 기술이 익숙해졌다. 2) 자료구조, 알고리즘, 프로그래밍 언어라는 큰 틀 안에서 관련 정보들을 정리하는 작업을 진행했었다. 덕분에 문제를 읽고 자료구조와 알고리즘을 선택하고, 이를 구현하기 위한 파이썬 언어 정보를 찾아보는 과정에 체계(?) 비스무리한 것이 생겼기 때문인 듯하다.
- 그래도 코딩 테스트는 나머지 20%를 채워 100%를 완벽하게 맞추어야 하는 문제다! 현재는 나머지 20%를 채워서 맞추는 문제도, 못채워서 못맞추는 문제가 랜덤하게 발생하지만, 세부유형별로 한 문제씩은 풀어서 경험을 많이 쌓는 방향으로 안정적인 100%를 만들어볼 생각이다.
오늘 푼 백준 문제들 정리
하노이 탑 이동 순서 11729번
11729번: 하노이 탑 이동 순서
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
1) 자료구조: 세 개의 장대가 각각 Stack 형태의 자료구조를 가진다. 맨 마지막에 들어간 원판이 가장 처음 장대에서 꺼내지는 형태이기 때문이다. 다만, 이 문제는 장대를 옮기는 과정에서 장대에 꽂혀있는 원판 정보를 물어보지 않았다. 따라서 장대의 자료구조는 쓸 필요가 없는 문제였다.
첨언으로, 자료구조는 컴퓨터에 정보를 효율적으로 저장하고 관리하는 데에 쓰이는 개념이다. 때문에 특정한 정보를 저장하고, 출력할 필요가 없는 문제들은 자료구조보다는 알고리즘으로 접근하는 게 좀 더 효율적인 방법인 것 같다. 일반적으로는 자료구조를 선택하고 어떤 알고리즘을 적용할지 선택한다. 반면, 특정 알고리즘이 고효율을 발휘하는 특정 연산에는 알고리즘을 선택하고 자료구조를 역선택한다. 특히, 반복이 많이 이루어지는 연산에서의 재귀 알고리즘이 그러하다.
2) 알고리즘: 반복 연산이 나타나는 문제였다. 이런 경우 가장 효율적인 알고리즘은 재귀 알고리즘이다. 이 문제의 핵심은 '반복연산'이기에 재귀 알고리즘을 떠올리고 자료구조를 역선택하는 게 편한 문제였다. 특히, 이 문제는 장대에 어떤 원반이 있는지를 묻지 않았고, '이동' 경로만을 묻고 있었기에 사실 자료구조 개념이 필요하지도 않은 문제였다.
3) Python 언어: 함수 안에서 다시 자기 자신(함수)를 부르는 재귀 함수를 사용해 문제를 해결한다. 재귀 함수를 사용할 때에는 꼭 조건문을 사용해 재귀 알고리즘이 끝나는 지점을 설정해두는 것이 중요하다. ( + 재귀 알고리즘은 while 문을 사용해서도 구현 가능하다. )
Stack 자료구조를 문제풀이에 사용하지는 않았지만 추가 설명을 해두자면, 파이썬이라는 프로그래밍 언어로 Stack 자료 구조를 구현하기 위해서는 파이썬의 리스트를 사용할 수 있다. Stack method로 사용하는 push, peek, pop 메쏘드들은 모두 append, len(), pop 등으로 대체해 사용할 수 있다.

4) 상세 코드 설명:
장대의 이동 규칙은 이러하다. 원반이 하나가 아니라면, 장대 1에서 장대 3으로 원반을 이동하고자 할 때 무조건 장대2에 가장 큰 원반을 제외한 원반들이 순서대로 쌓이게 된다. 원반이 3개일때는 장대 2에 원반 1, 2가 순서대로 쌓인다. 원반이 4개일 때는 장대 2에 원반 1, 2, 3이 순서대로 쌓인다(원반 숫자가 클 수록 큰 원반이라 가정하고 설명하겠다.) 원반이 5개일 때는 장대 2에 원반 1, 2, 3, 4가 쌓인다. 반복이 된다. 이 부분이 우리가 재귀 알고리즘을 적용할 수 있는 포인트다.
- 가장 큰 원반을 제외한 원반들을 '시작지점도 도착지점도 아닌곳'으로 옮기는 재귀함수
- 큰 원반이 도착지점으로 이동할 수 있게 되었다! 큰 원반을 도착지점으로 옮기는 print 문
- 중앙에 위치한 원반들을 도착지점으로 옮겨서 완성해주는 재귀함수
가장 상위에 불러진 input 값에 해당하는 1 , 3 이라는 매개 변수에 맞추어 원반 두개(원반 1, 2)를 2 장대로 옮기는 재귀함수가 불러지고, 마지막에는 원반 두개(원반 1, 2)를 3장대로 옮기는 재귀함수가 불러진다.
여기서 정의되어진 함수는 시작점에 위치한 원반을 도착지점으로 옮기는 수식이다. 따라서 새롭게 생성된 move (2 ,1 ,2)에서는 두 개의 원반이 2에 도착하기 위한 수식이 다시 재귀적으로 삽입된다. 이때 중간다리로 활용하는 장대는 3이되고, 따라서 큰 원반을 제외한 작은 원반이 '시작지점도 도착지점도 아닌 곳'에 해당하는 장대3에 쌓이게 된다. 이후 큰 원반이 시작점에 해당하는 장대 1에서 도착점에 해당하는 장대 2에 쌓인다. 마지막으로 장대3에 위치해있는 작은 원반이 도착지점인 장대 2에 쌓이게 된다.
이렇게 n =1 이 될때까지 시작점, 시작점도 도착점도 아닌 곳, 도착점을 계속 바꿔가며 원반들이 이동하고, n =1이 된다면 재귀 함수를 적용할 필요 없이 바로 도착점으로 이동하며 값이 반환된다.
move (2, 1, 2) --> 탑 두개를 1에서 2로 이동해라
move (1, 1, 3)
print (1, 3)
print (1, 2)
move (1, 3, 2)
print (3, 2)
print (시작점, 이동할 점)
move (2, 2, 3 ) --> 탑 두개를 2에서 3으로 이동해라
move (1, 2, 1)
print(2, 1)
print (2, 3)
move (1, 1, 3)
print(1, 3)
좌표 정렬하기2 11651번
11651번: 좌표 정렬하기 2
첫째 줄에 점의 개수 N (1 ≤ N ≤ 100,000)이 주어진다. 둘째 줄부터 N개의 줄에는 i번점의 위치 xi와 yi가 주어진다. (-100,000 ≤ xi, yi ≤ 100,000) 좌표는 항상 정수이고, 위치가 같은 두 점은 없다.
www.acmicpc.net
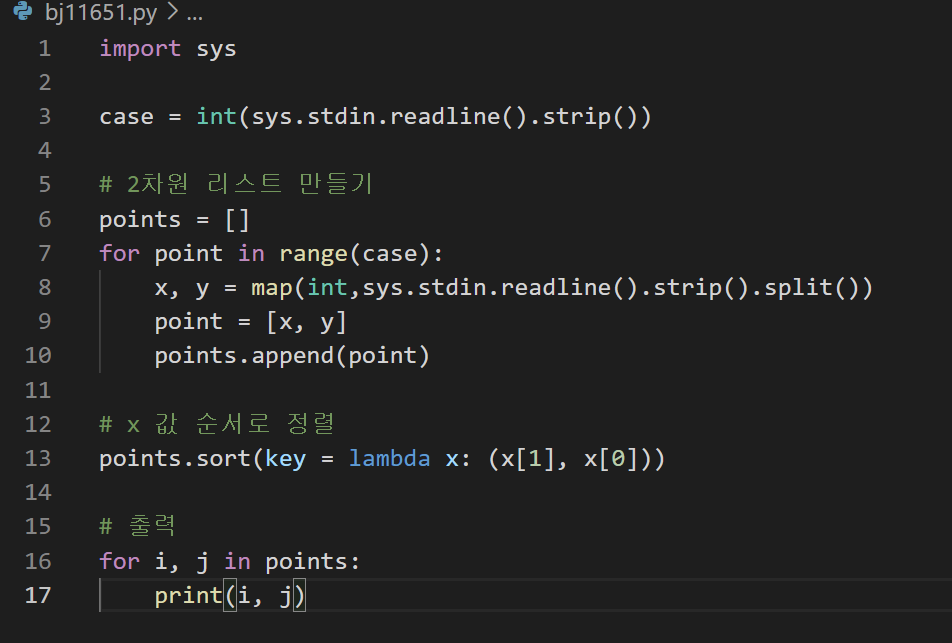
1) 자료구조: 저장형태로 이차원 리스트를 활용해야 좋은 문제였다. 두 개씩 묶여진 값들이 하나의 좌표로 활용되기 때문에 두 값을 하나로 묶어줄 리스트가 필요했고, 또 이들을 다시 정렬해야 했기 때문에 리스트를 담는 리스트가 필요했기 때문이다.
2) 알고리즘: 오히려 알고리즘이 중요하지 않은 문제였다. 사실, 정렬이라 함은 알고리즘의 가장! 중요한! 부분이나, 정렬을 위해 만들어진 프로그래밍 함수를 사용하지 않고 정렬을 구현하는 것은 코드 상 비효율적인 부분이 있다.
그래서 파이썬의 sort, sorted 놔두고 왜 정렬 개념을 공부하는 지 그 목적이 궁금했다. 나중에 이 개념을 직접 활용해 코드를 짜야하는 상황이 있는지, 아니면 최소한의 개념은 알고 있어야 한다는 의미로 공부하는 것인지는 아직 모르겠다.
3) Python 언어: 파이썬의 함수인 sort와 lamda를 이용해 오름차순 정리했다. 정말 여러가지 복잡한 정렬 알고리즘을 함수 하나로 해결...!
나무 자르기 2805번
2805번: 나무 자르기
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000) 둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보
www.acmicpc.net
1) 자료구조: 이 문제는 정보 저장보다는 주어진 데이터에서 값을 추출하는 알고리즘이 더 중요했기에 자료구조는 중요한 부분이 아니었다.
2) 알고리즘: 1,000,000,000 개나 되는 데이터를 검사해야 했기 때문에 검색 알고리즘에 해당하는 선형검색, 이진검색, 해시법 중 이진 검색을 선택해서 풀어야 효율성을 극대화 할 수 있는 문제이다. (선형 검색은 당연히 아니고... 해시법도 이 경우에는 정해지지 않은 데이터를 하나 찍어 해당 상황에서 발생하는 값을 계산해야하는 성격이 있었기 때문에 어울리지 않는 듯 하다.)
3) Python 언어: 이진 검색알고리즘은 while문을 활용해 구현할 수도있고, 재귀 함수를 활용할 수도 있었지만 난 while문을 활용했다. 재귀함수 아직 안익숙해요... 쓰다보니 재귀 알고리즘 구현 시 사용하는 프로그래밍 언어랑 똑같은데..? 이진 검색도 나름 반복연산이라 재귀 알고리즘 하위로 포함 될 수 있을 것 같다.
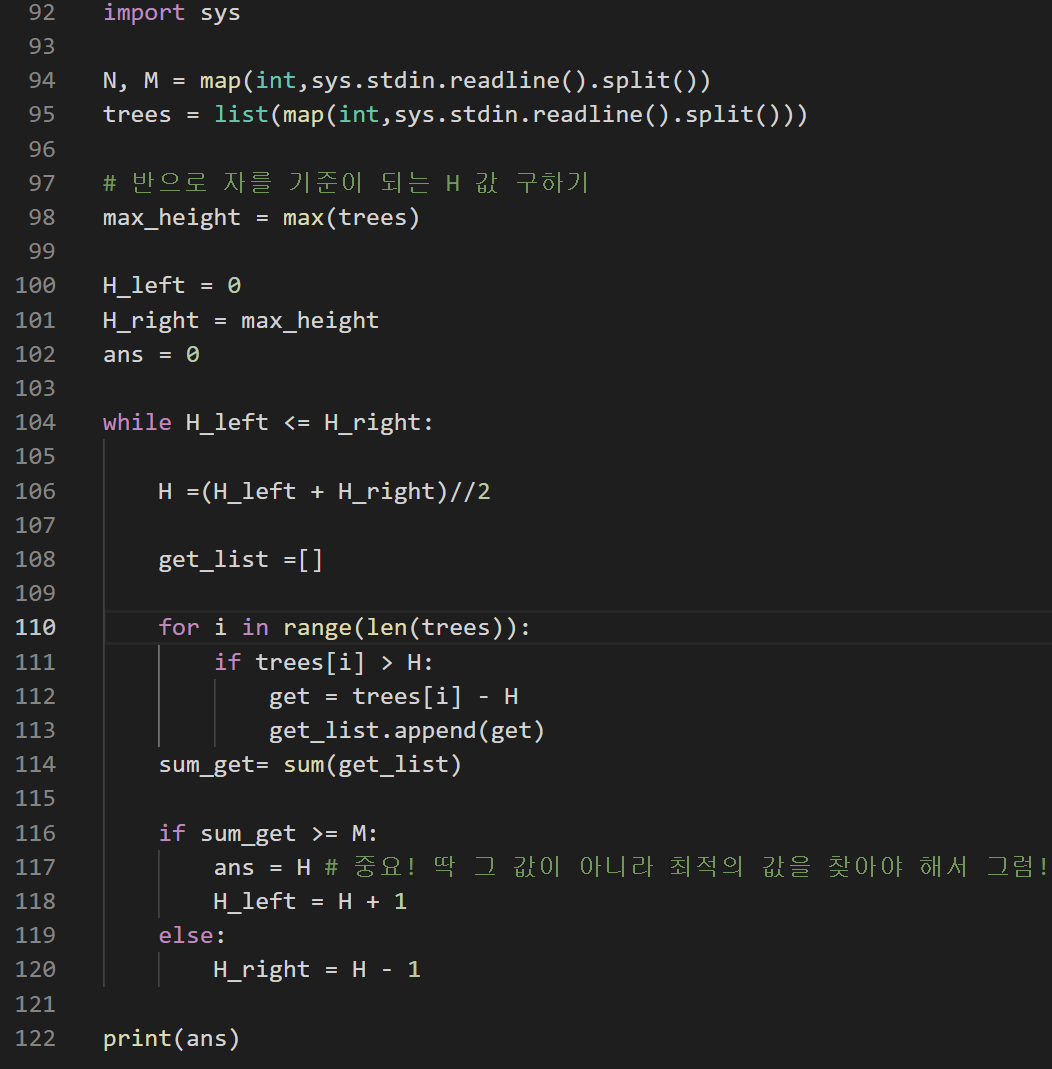
4) 코드 이모저모:
이 문제는 내가 20%를 완성 못한 문제였다. 이유는 102줄에 해당하는 ans =0 과 117 줄에 해당하는 ans = H를 안넣고 바로 print(H)해버렸기 떄문이다. 일반적인 이진 검색과 달리 이 문제는 찾고자 하는 값이 리스트에 들어있는 딱 "그 값"이 아니다... 따라서 바로 H를 출력해버리면 찾고자 하는 H에서 본의 아니게 while문을 한번 더 돌아버린 H가 출력되어 오류가 발생한다. (기억하고 있어야 하는 상세 유형 풀이 이다)
'Basic > 자료구조와 알고리즘 Algorithm' 카테고리의 다른 글
| 나의 알고리즘 공부 여정6 - 탐색 알고리즘, 코드 기능과 형태 개선 (1) | 2021.03.16 |
|---|---|
| 나의 알고리즘 공부 여정5 - 시간 복잡도, 코드 효율화 (0) | 2021.03.12 |
| 나의 알고리즘 공부 여정4 - DFS, BFS, Dynamic Programming, 유형별 개념 적용 (0) | 2021.03.11 |
| 나의 알고리즘 공부 여정3 - 스택과 큐, 풀이의 유사성 (0) | 2021.03.10 |
| 나의 알고리즘 공부 여정1 - 우리는 왜 알고리즘을 공부하는가? (0) | 2021.03.08 |